
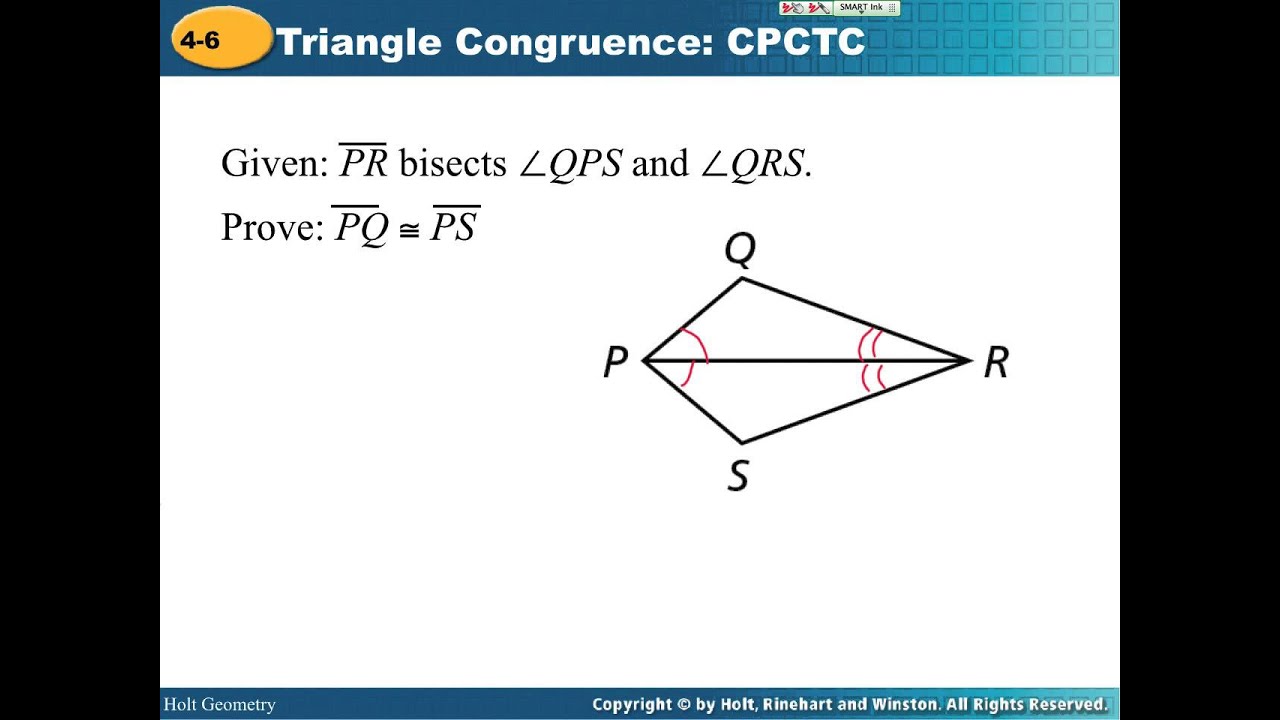
It means that the first angle of one triangle is congruent to the first angle of the other, the second to the second, and so on. In congruent triangles, the corresponding parts are equal in measurement.

The term ‘corresponding parts’ refers to the sides and angles in a triangle that occupy the same relative position. For two triangles to be congruent, they must satisfy one of the following conditions: Side-Side-Side (SSS), Side-Angle-Side (SAS), Angle-Side-Angle (ASA), Angle-Angle-Side (AAS), or Right angle-Hypotenuse-Side (RHS) congruence rules. The concept of congruent triangles is fundamental in understanding CPCTC. If you were to place one triangle on top of the other, they would match perfectly. In geometry, congruent triangles are triangles that are identical in terms of size and shape. The corresponding sides (the equal lengths) and angles (the equal corners) of these cookies would be exactly the same, and that’s precisely what CPCTC is all about! Congruent Triangles Imagine two identical triangle-shaped cookies. This principle is widely used in proofs and problem-solving in geometry. So, let’s delve deeper and understand the concept of CPCTC.ĬPCTC is a principle in geometry that affirms that if two triangles are congruent, then their corresponding parts – the sides and angles that match – are also congruent. It is used in various real-life scenarios such as architecture, engineering, and even in art. Understanding CPCTC can be a big step in your journey to mastering geometry.

In simpler terms, if two triangles are congruent (exactly the same in size and shape), then their corresponding parts (sides and angles) are also congruent. If you’re wondering, ‘What does CPCTC stand for?’, it’s an abbreviation that stands for Corresponding Parts of Congruent Triangles are Congruent. One of the most interesting concepts in geometry is CPCTC. Geometry is a fascinating area of mathematics that involves shapes, sizes, and properties of space. That’s why it’s crucial for our students to grasp the essence of CPCTC, which establishes the congruence of corresponding parts in congruent triangles. Geometry, with its intricate shapes and spatial relationships, plays a vital role in numerous real-life applications, from designing buildings to creating stunning works of art.
By understanding this fundamental principle, our young mathematicians at Brighterly will develop a solid foundation in geometry, logical reasoning, and problem-solving skills. In this article, we will embark on a journey through the definition, postulates, theorem, proof, and examples of CPCTC. At Brighterly, we believe in making math accessible, engaging, and tailored for young minds. Welcome to Brighterly, where learning mathematics is an exciting adventure! Today, we invite you to delve into the captivating world of geometry as we explore the concept of CPCTC – Corresponding Parts of Congruent Triangles are Congruent.


 0 kommentar(er)
0 kommentar(er)
